Background

I was first introduced to quantization after grad school, while working at a ML chip accelerator company. My work there centered around a challenge that many modern ML models face - they're very expensive to run. On a local device like a car or a phone with limited compute capabilities, running a large computer vision or language model can be very slow, consume too much energy, or simply not fit in the available memory. Making API calls to a cloud-based models has its own problems - high cost, latency, and lack of data privacy or model customization.

Generally, we were given a pre-trained model from a customer company or client, with the goal to make it run on our custom chip. The chip could run models at a high efficiency^[1] using some smart engineering to design an efficient primary processor, instruction scheduler, and memory transfers. However, to achieve more efficient processing, we needed to change the model a little - instead of maintaining the parameters and activations in high precision (typically 16-32 bit floating points), they had to be compressed to 8-bit integers. This would accelerate memory transfers and matrix multiplications^[2], letting us hit higher efficiency numbers and stay competitive.

So far so good, right? Here's the kicker - when we reduced the bit precision of our model values, they would often lose a huge amount of performance on the tasks they were trained for. Sometimes the accuracy^[3] drop would be a few percentage points, but this drop could be as large as 50% or more, indicating the model is completely losing all the knowledge it learned in training. Worse still, although some models were known to be more susceptible, these variations were highly unpredictable.

Luckily, we weren't the only ones to be facing this issue. Everyone from Nvidia to Google had run against this wall, coming up with new methods and training strategies to help. Researchers also noticed some underlying issues that could be mitigated somewhat cheaply given a pre-trained model in full precision. The umbrella term to encapsulate these approaches came to be known as 'post-training quantization' (PTQ). I got to test a lot of these methods, and as I did I grew increasingly curious about the general problem of quantization. The problem seems to give us insights about the loss landscape, model training dynamics, and the central problem in ML - how can we learn computationally efficient representations of a set of data and task^[4].

To be clear, PTQ is not the only approach to quantization. Exciting new techniques are emerging to focus on low-precision model training (FP8 Training), intermediate solutions like quantization-aware training (QAT) and quantized fine-tuning (QLoRa). I hope to use this deep dive to explore current state-of-the-art approaches, ass well as explanations for what seems to be happening in the quantized regime. I'll also be tackling problems that give a lay of the land, even if they're not directly related.

The general problem of model compression and optimization has led to an explosion of fascinating work outside of quantization. These range from optimizing the methods of memory storage and transfer for activations (eg, flash-attention), building faster kernels that can perform the linear algebra of ML more efficiently, distilling and pruning models, to developing of entirely new models based on classical signal processing theory (SSMs). Broadly, these fall into hardware and software optimizations (I clump model changes into the software category). We’ll be exploring many of these ideas, with a bias towards model-centered techniques. Part of the reason for this is practical - working at the hardware level is fairly difficult to do without a good amount of prior setup, hardware navigational skill, and actually reliable hardware to tinker with. The other is that I’m simply more interested in the work on the ML side right now, although I might attempt to explore hardware in the future!

Basics of Quantization

Here we provide a brief definition of quantization. Simply put, it's the process of discretizing a continuous (aka higher precision) spectrum of values using a chosen scheme. This process bins values into designated groupings, compressing the number of representations (aka bytes) that are used to store all the data. A simple quantization scheme is roundToNearestInteger(float val), that rounds any real valued number to the closest integer. In this approach, the values 3.05, 3.003, and 3.49 all round to 3. As you can see, we tend to lose precise information about our values for the tradeoff of less memory consumed. Refer to Visualizing Quantization as a great resource to visualize how quantization works.

The first topic we'll work on will rely on fixed point (aka integer) quantization, so we detail this approach below.

Fixed-Point Quantization

The process for fixed-point/integer quantization is as follows: Suppose we have a group of values (eg, a model weight tensor). If we wish to compress values to $n$ bits, we have $2^n-1$ equally sized bins to put our values in. We can use the range of values present in our tensor to decide how big our bin/grid size should be. There are many great references explaining how the fixed-point quantization process works, such as here, here, and here. A general form of the quantization process is shown below. Given a tensor (or any group of values $X$), we first use the range of $X$ to calculate the quantization bin size $q$. We then calculate the bin in which $0$ falls into^[5], and use the third equation to actually quantize a number $x$ into a quantized integer $x_q$. Note that once we have $x_q$, the only way we can find the original value $x$ is with the quantization parameters $q$ and $zp$.

Without going into too much detail, matmul.

We don't have to stick to one tensor as our group. If we wanted we could take all of our model's weights and activations^[6], calculate a bin size and quantize all the values into these bins. However, numerical values across the model can range wildly across multiple orders of magnitude, so this approach will result in a huge quantization error. On the other hand, in theory we could 'quantize' each and every term individually with individual quantization parameters $q$ and $zp$. However, these would then need to be propagated through the network, adding a huge compute cost.

Clearly, we need to find a balance with the level of granularity of our groups. Through experiment and a study of hardware operator flow, engineers have found that the optimal granularity is different for weights and activations. For activations, the best balance is to make each intermediate activation tensor into a group, and quantize appropriately. For weights, however, we can get away with a more granular approach, and perform per-channel/neuron quantization. This is best explained visually, as can be seen in Figure 1.

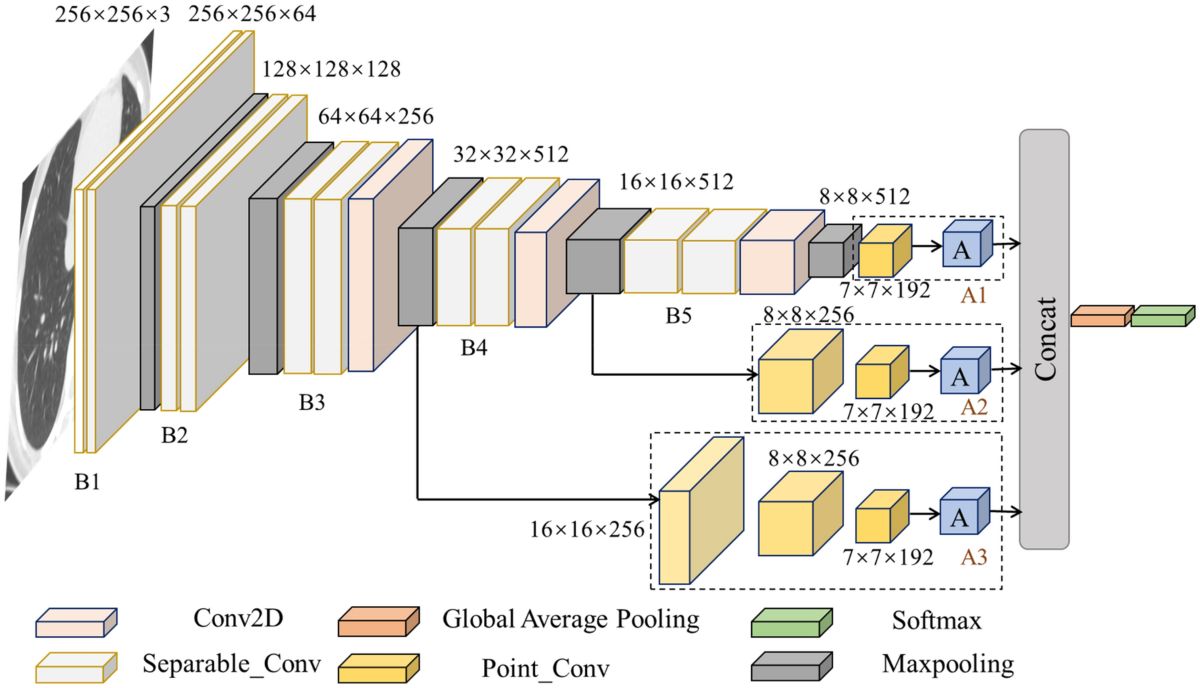
Figure 1. A cross section for a convolutional neural network. Each of the blocks (B1, B2, etc.) are intermediate activations, where one block corresponds to one tensor. Each strip within a block is one channel (eg there are 64 channels in B1). Although not shown here, the weights that propagate the activations through the network have a corresponding set of channels, corresponding to the output activation channels (eg, between B1 and B2 there are 128 weight tensors, one for each output channel of B2).

Even for a given group (channel/tensor), we don't have to use the min and max values to quantify our range. There are more sophisticated methods that can clip outlier values, or simpler methods that use $(mi{n}_X=-ma{x}_{|X|}$). The latter is called symmetric quantization, and offers the simplicity of eschewing the zero-point parameter. More details about integer quantization methods can be found in (Wu et al, 2020).

Footnotes